In machine learning, it is often required to compute gradients of a loss function for stochastic optimization and sometimes these loss functions are expressed as an expectation. For example, in variational inference (converting an inference problem in a probabilistic model to an optimization problem), we need to compute the derivative of the ELBO loss which is written in terms of an expectation. Another example is the policy gradient algorithm in reinforcement learning where the objective function is the expected reward. REINFORCE and reparameterization trick are two of the many methods which allow us to calculate gradients of expectation of a function. However both of them make different assumptions about the underlying model and data distributions and thus differ in their usefulness. This post will introduce both methods, and in the process, draw a comparison between them. There are multiple tutorials which already cover REINFORCE and reparameterization gradients but I’ve often found them in context of specific models like VAEs or DRAW which slightly obfuscates the general picture of these methods. Shakir Mohamed’s blog also covers these topics in an excellent way and I would highly advise everyone to go check it out.

The setup

Given a random variable $x \sim p_{\theta}(x)$ where $p_{\theta}$ is a parametric distribution and a function $f$, for which we wish to compute the gradient of its expected value, the quantity of interest is:

$$\nabla_{\theta}\mathbb E_{x\sim p_{\theta}(x)}[f(x)]$$

For an optimization problem, the above refers to the derivative of the expected value of the loss function. The difficulty in evaluating this term is that in the general case, the expectation is unkown and the derivative is taken wrt the parameters of the distribution $p_{\theta}$.

REINFORCE

The REINFORCE algorithm [¹] also known as the score function estimator [²] uses a simple differentiation rule called the log-derivative trick which is simply the differentiation rule for the logarithm.

$$\nabla_{\theta}p_{\theta}(x) = p_{\theta}(x) \nabla_{\theta}\log p_{\theta}(x)\tag{1}$$

Although written as above, the ‘trick’ seems very plain, it is very useful in situations where $p_{\theta}$ is the likelihood for a random variable (also, likelihoods often belong to exponential families which makes the expression on the right more amenable). The term $\nabla_{\theta}\log p_{\theta}(x)$ is called the score and regularly comes up in maximum likelihood estimation. It also has many wonderful properties like having zero expected value (which proves useful when using it for variational inference among other things).

With this, we get back to our problem of estimating the gradient. Using the definition of expectation,

$$ \begin{align} \nabla_{\theta}\mathbb E_{x\sim p_{\theta}(x)}[f(x)] & = \nabla_{\theta}\int{f(x)p_{\theta}(x)dx}\tag{2}\\ & = \int{f(x)\nabla_{\theta}p_{\theta}(x)dx}\tag{3}\\ & = \int{f(x)p_{\theta}(x) \nabla_{\theta}\log p_{\theta}(x)dx}\tag{4}\\ & = \mathbb E_{x\sim p_{\theta}(x)}[f(x)\nabla_{\theta}\log p_{\theta}(x)]\tag{5}\\ \end{align} $$

The reason why the integral and differentiation can be switched in the equation $3$ is because of the Leibniz Integral rule. Equation $4$ is just the application of the log-derivative trick from equation $1$. Now, since we know the distribution under the expectation, we can use Monte Carlo sampling to approximate the expectation.

$$\approx \frac{1}{N}\sum_{i=1}^{N} f(x_i)\nabla_{\theta}\log p_{\theta}(x_i)\tag{6}$$

Note that the above is an unbiased estimator of the gradients (expected value of the gradient is the same as the true gradient), and hence optimization with such gradients can converge to a local optima following the Robins-Munro conditions. The score function estimator assumes it is possible to cheaply sample from the distribution $p_{\theta}(x)$. It’s also interesting to note that REINFORCE places no restriction on the nature of the function $f$ and it doesn’t even need to be differentiable for us to estimate the gradients of its expected value.

Of course, the unbiased estimates also mean that the variance for these gradients are very high. This can be thought of as a result of sampling values of $x$ which are rare. To counter this, a common solution is to use something called control variates. The basic idea is to replace the function under the expectation with another function which has the same expected value but lesser variance. This can be done by subtracting from the original function, a term which has its expectation as zero. Many other solutions like Importance Sampling or Rao-Blackwellization can also be used for variance reduction. Refer to chapter 8, 9 and 10 of this book for details on those methods.

Reparameterization trick

Recall that our object of interest is the gradient of the expected value of the function.

$$\nabla_{\theta}\mathbb E_{x\sim p_{\theta}(x)}[f(x)]$$

Also recall that the problem in evaluating this quantity is the fact that the expectation is taken wrt a distribution with parameters $\theta$ and we can’t compute the derivative of that stochastic quantity. Reparameterization gradients also known as pathwise gradients allow us to compute this by re-writing the samples of the distribution $p_{\theta}$ in terms of a noise variable $\varepsilon$, that’s independent of $\theta$. More concretely,

$$ \begin{align} \varepsilon & \sim q(\varepsilon)\tag{7}\\ x & = g_{\theta}(\varepsilon)\tag{8}\\ \nabla_{\theta}\mathbb E_{x\sim p_{\theta}(x)}[f(x)] & = \nabla_{\theta}\mathbb E_{\varepsilon\sim q(\varepsilon)}[f(g_{\theta}(\varepsilon))]\tag{9}\\ & = \mathbb E_{\varepsilon\sim q(\varepsilon)}[\nabla_{\theta}f(g_{\theta}(\varepsilon))]\tag{10}\\ \end{align} $$

Thus, x is reparameterized as a function of $\varepsilon$ and the stochasticity of $p_{\theta}$ is pushed to the distribution $q(\varepsilon)$ where $q$ can be chosen as any random noise distribution, eg a standard Gaussian $\mathcal{N}(0,1)$. An example of such reparameterization can be highlighted by assuming $x$ is sampled from a Gaussian, $x \sim \mathcal{N}(\mu,\sigma)$. The function $g_{\theta}(\varepsilon)$ then can be defined as the following:

$$g_{\theta}(\varepsilon) = \mu_{\theta} + \varepsilon\sigma_{\theta}$$

where $\varepsilon \sim \mathcal{N}(0,1)$

The figure below taken from Jaan’s blog shows it succinctly for the case of a VAE (he uses $z$ as the random variable instead of the $x$ I have been using). Circles are stochastic nodes whereas diamonds are deterministic nodes.

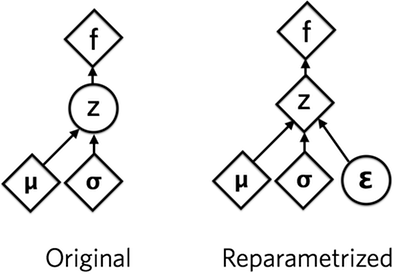
As evident from equation $10$, the reparameterization has changed the expectation to a distribution independent of $\theta$ and can now be computed using Monte Carlo provided $f(g_{\theta}(\varepsilon))$ is differentiable wrt $\theta$.

$$\nabla_{\theta}\mathbb E_{x\sim p_{\theta}(x)}[f(x)] \approx \frac{1}{N}\sum_{i=1}^{N} (\nabla_{\theta}f(g_{\theta}(\varepsilon_i)))$$

Reparameterization gradients have been shown to typically have lower variance than REINFORCE gradients or even REINFORCE with control variates (for example, in variational inference [³]). But they do have requirements of having differentiable functions as shown above.

Summary of differences

The key differences between the two gradient estimation techniques are summarized in the table below.

Properties	REINFORCE	Reparameterization
Differentiability requirements	Can work with a non-differentiable model	Needs a differentiable model
Gradient variance	High variance; needs variance reduction techniques	Low variance due to implicit modeling of dependencies
Type of distribution	Works for both discrete and continuous distributions	In the current form, only valid for continuous distributions
Family of distribution	Works for a large class of distributions of x	It should be possible to reparameterize x as done above

References